Лекция 10. Интегрирование уравнений Эйлера
Интегрирование уравнений Эйлера рассмотрим на широко распространённом примере движения жидкости под действием силы тяжести. Примерами такого движения могут служить: течение реки, ручья или любого другого потока жидкости, течение жидкости в водопроводе, работающем от водонапорной башни.
Движение жидкости описывается обобщённой формой уравнений Эйлера

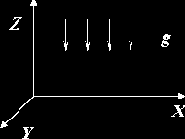

принимает вид:

где g – ускорение свободного падения.
Подставив это выражение в уравнение Эйлера, и умножив на «–1», для того, чтобы избавиться от знаков «минус» перед каждым слагаемым, получим:

После интегрирования придём к виду:

где C – постоянная интегрирования (знак «-» перед ней не имеет
физического значения и поставлен только для удобства последующих математических преобразований).
Разделив последнее равенство на g, придём к окончательному виду:

Полученное выражение называется интегралом Бернулли, а постоянная величина H носит название гидродинамический напор или полный напор. Другое название интеграла Бернулли, которое применяется значительно чаще, - уравнение Бернулли для струйки идеальной жидкости.
